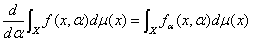積分の諸性質
Riemann積分とLebesgue積分
狭義の意味でRiemann積分可能ならば、Lebesgue積分可能
広義の意味でRiemann積分可能であっても、Lebesgue積分可能とはかぎらない
積分法の第1平均値定理
集合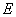 で
で
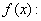 有界、
有界、
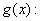 積分可能
積分可能
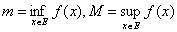
とおくと、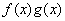 は
は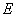 で積分可能
で積分可能
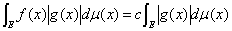
を満たす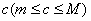 が存在する
が存在する
Lebesgueの収束定理
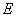 で
で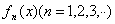 が
が -可測
-可測
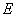 で積分可能な関数
で積分可能な関数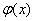 が、
が、
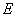 の各点で
の各点で
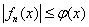
ならば、
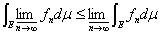
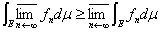
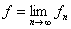 ならば
ならば
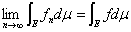
積分と微分
測度空間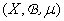 上の関数
上の関数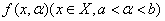
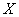 で可積分、
で可積分、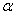 で微分可能
で微分可能
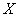 で積分可能な関数
で積分可能な関数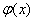 が、
が、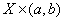 で
で
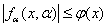 ならば、
ならば、
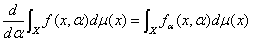
[0]Top
こだわりハウス
ピンポイントストリートビュー
おもしろ画像のピンポイントストリートビュー
Excel Vba テクニック集
Excel 計算式解析・他解析
富山の建築家
Excel 計算式解析・他解析
積分の定義・積分の記号の意味の研究
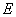 で
で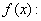 有界、
有界、
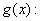 積分可能
積分可能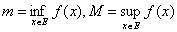
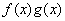 は
は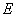 で積分可能
で積分可能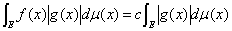
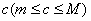 が存在する
が存在する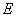 で
で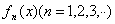 が
が -可測
-可測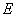 で積分可能な関数
で積分可能な関数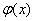 が、
が、
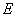 の各点で
の各点で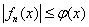
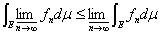
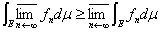
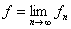 ならば
ならば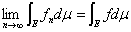
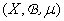 上の関数
上の関数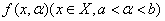
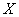 で可積分、
で可積分、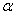 で微分可能
で微分可能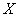 で積分可能な関数
で積分可能な関数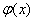 が、
が、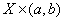 で
で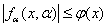 ならば、
ならば、