前提条件
オイラーの考え方を説明する。数学の記号は、一部現代の表記方法を使用する。
例
| 名称 | 原書 | 現代表記 |
| 組合せの記号 | なし | 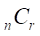 |
| 複素数 | 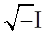 注: 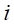 は自然数の変数 は自然数の変数
|
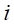 |
| 十分に大きな自然数 | 言葉で説明 | 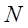 |
| 階乗 | 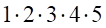 | 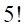 |
| 数列 | 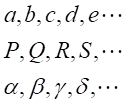 | 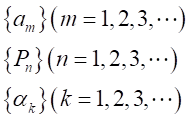 |
| 数列の加算 | 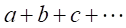 | 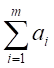 |
自然対数e
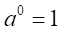
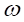 を十分に小さい正の数とする。
を十分に小さい正の数とする。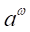 は1より少し大きい数となる。
は1より少し大きい数となる。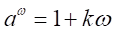 を満たす
を満たす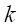 が存在する。
が存在する。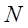 を十分に大きな自然数とする。
を十分に大きな自然数とする。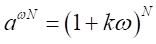
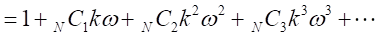
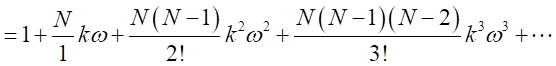
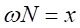 とおく。
とおく。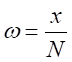 、
、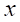 は正の実数となる。
は正の実数となる。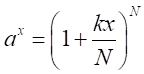
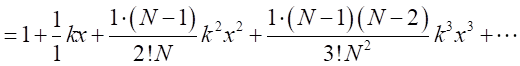
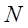 が十分に大きな自然数なので、
が十分に大きな自然数なので、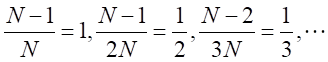 となる。 注:この証明はない。
となる。 注:この証明はない。これを代入すると、
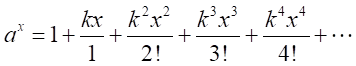
となる。
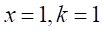 とすると、
とすると、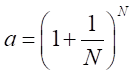 、
、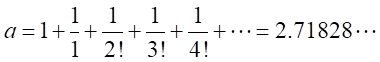
ここで、
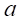 を
を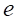 と表記する。注:
と表記する。注: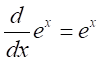 という性質は記載されていない。
という性質は記載されていない。
三角関数の級数表示
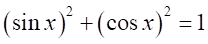 より、
より、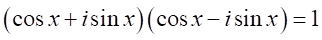
そして、一般的に
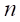 を自然数として、
を自然数として、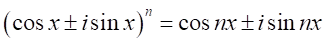 となる。
となる。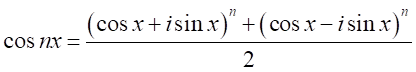
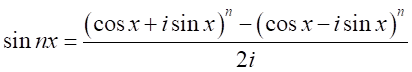
それぞれを展開すると、
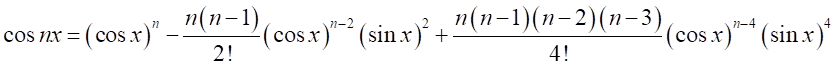
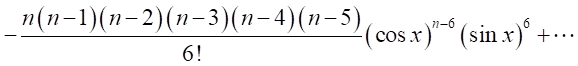
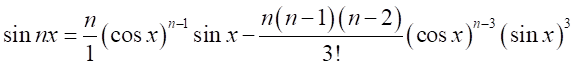
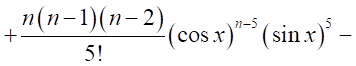
円の半周は180°である。ここで、円の半周を弧長
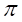 とする。
とする。十分に小さい正の実数
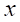 に対して、
に対して、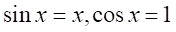 とできる。注:
とできる。注: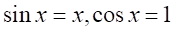 の証明は記載されていない。
の証明は記載されていない。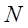 を十分に大きな自然数とする。
を十分に大きな自然数とする。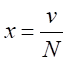 とおく。
とおく。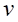 は実数となる。
は実数となる。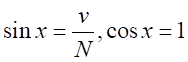
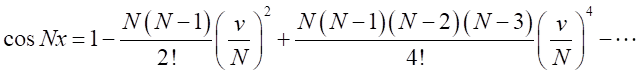
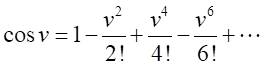
同様に、
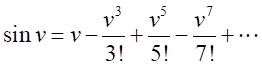

オイラーの公式の導入
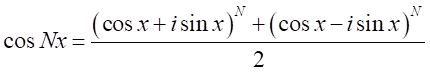
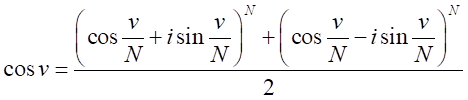
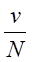 は十分に小さい数なので、
は十分に小さい数なので、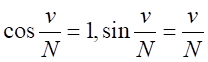 とおける。したがって、
とおける。したがって、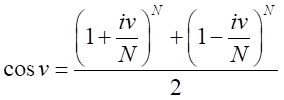
となる。同様に、
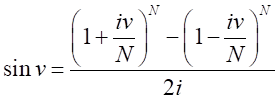
ところで、
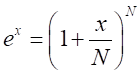 なので、
なので、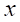 の代わりに
の代わりに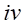 と表記し、
と表記し、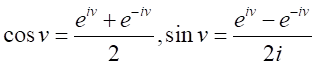
となる。したがって、
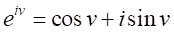 となる。 注:
となる。 注: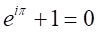 の説明はない。
の説明はない。
整関数の因子
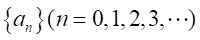 を実数の無限数列とする。
を実数の無限数列とする。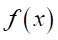 を無限次の多項式とする。
を無限次の多項式とする。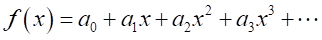
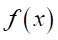 の因数(因数分解)を考える。
の因数(因数分解)を考える。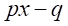 の因数を持つならば、
の因数を持つならば、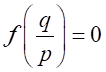 となる。
となる。上記は実数解の場合だが、虚数解の場合について考える。
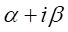 が解であれば
が解であれば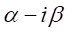 も解なので、
も解なので、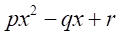 の因数を持つと仮定する。
の因数を持つと仮定する。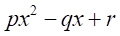 が虚数解を持つのであれば、
が虚数解を持つのであれば、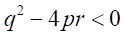
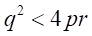
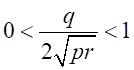
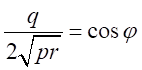 、を満たす
、を満たす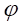 が存在する。
が存在する。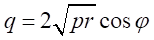
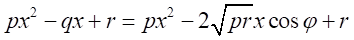
ここで、式中の
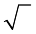 表示をさけるため、
表示をさけるため、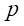 を
を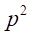 と、
と、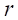 を
を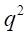 と書き直す。
と書き直す。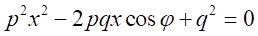 とすると、
とすると、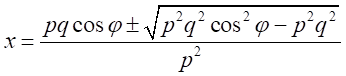
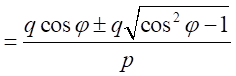
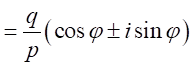
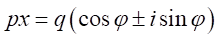
したがって、
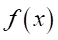 は
は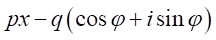 と
と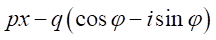 の因数を持つ。
の因数を持つ。一般的に
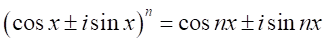 となるので、
となるので、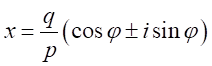 、
、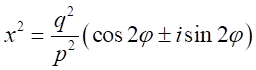 、
、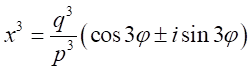 、・・・
、・・・
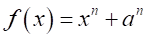 の因数
の因数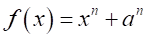 の虚数解による因数を考える。
の虚数解による因数を考える。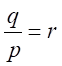 とおくと、
とおくと、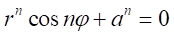 、
、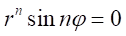 という2つの方程式ができる。
という2つの方程式ができる。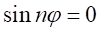 となるのは、
となるのは、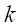 を整数とした場合に
を整数とした場合に
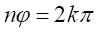 又は
又は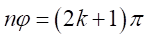 のときである。
のときである。ところで
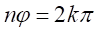 とすると
とすると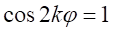 、
、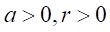 なので矛盾がでる。
なので矛盾がでる。したがって、
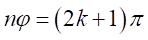 としなければならない。
としなければならない。したがって、虚数による因数の式は
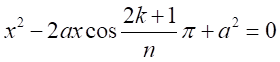 の解である。
の解である。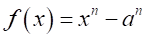 の場合の因数は、
の場合の因数は、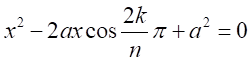 の解である。
の解である。
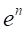 の因数
の因数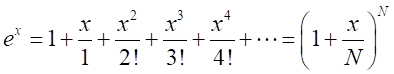
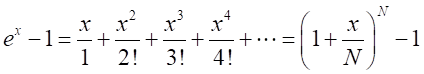
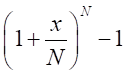 は
は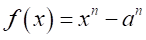 と同じ形式なので、
と同じ形式なので、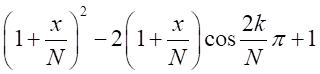
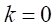 とすると、
とすると、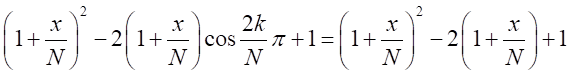
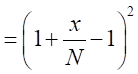
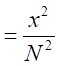
したがって、
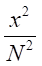 の因数を持つ。
の因数を持つ。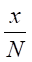 が微小であることから、
が微小であることから、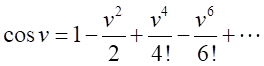 において、
において、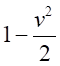 の右側の項、
の右側の項、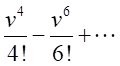 は無視できる。
は無視できる。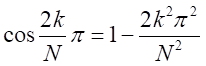 とできる。
とできる。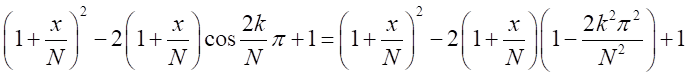
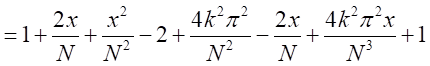
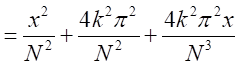
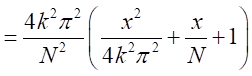
したがって、
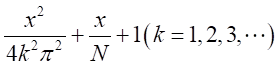 という無限個の因数を持つので、
という無限個の因数を持つので、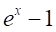 は、
は、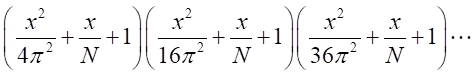
という因数を持つ。

三角関数の因数
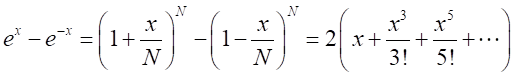
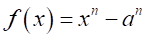 の場合の虚数による因数の式が、
の場合の虚数による因数の式が、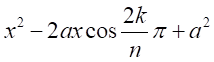 となることから、
となることから、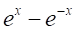 の因数の式は、
の因数の式は、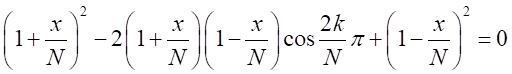 となる。
となる。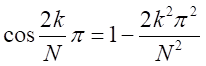 となるので
となるので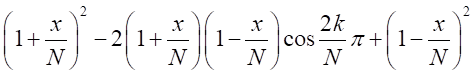
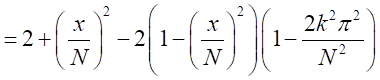
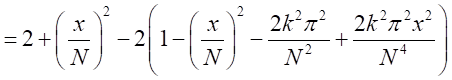
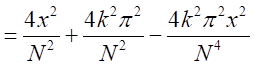
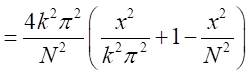
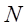 が十分に大きいので
が十分に大きいので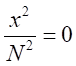 とできる。
とできる。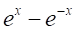 は、
は、 で割り切れる。
で割り切れる。第1因子が
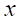 となるので、
となるので、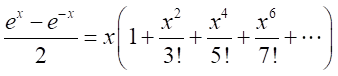
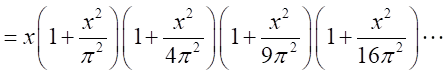
同様に、
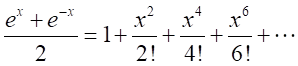
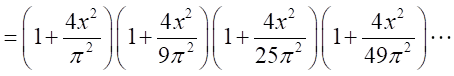
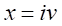 とおくと、
とおくと、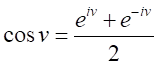
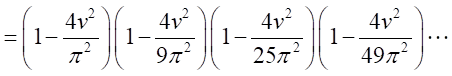
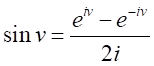
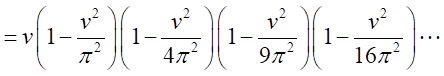

整関数、積による表示
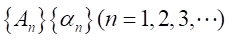 を有限又は無限数列とする。
を有限又は無限数列とする。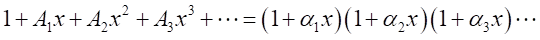
とする。
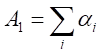
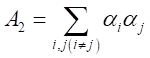
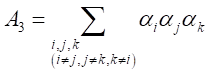
・・・・・・・
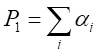
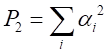
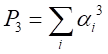
・・・・・・・・
とする。
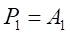
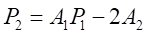
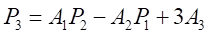
・・・・・・・
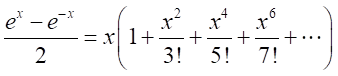
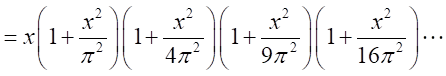 より、
より、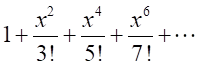
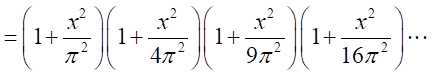
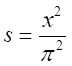 とおくと、
とおくと、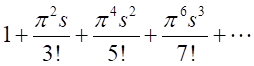
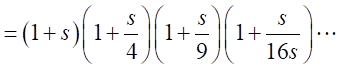
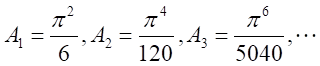
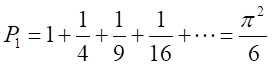
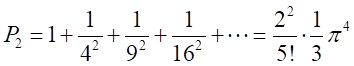
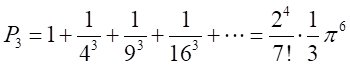
・・・・・・
このことから、
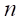 を自然数として、
を自然数として、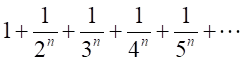 という一般的な級数が想定できる。
という一般的な級数が想定できる。
円周率と素数の関係
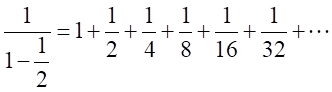
この式では、2のべき乗のみが現れる。
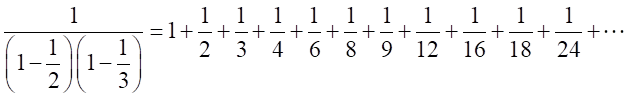
この式では、2のべき乗、3のべき乗、及びその積のみが現れる。
したがって、左辺にすべての素数を使うと、右辺にはすべての自然数が現れる。
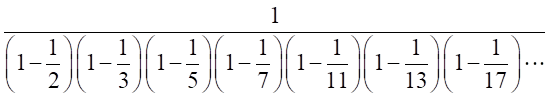
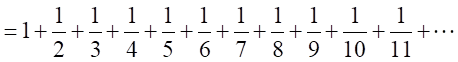
さらに、素数のべき乗の場合も同様な式になる。
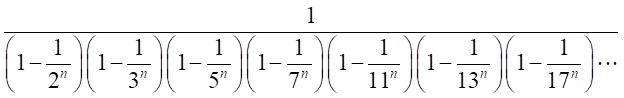
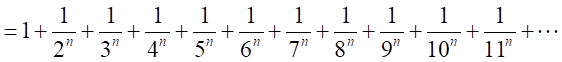
これを応用すると、
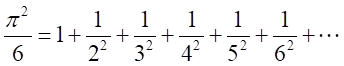
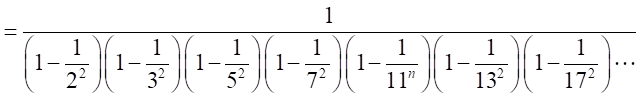
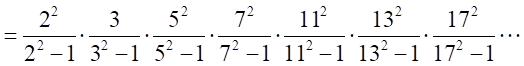
のように、円周率が、すべての素数による演算の積で表現できる。

