Natural and Integer Numbers
Natural number
Peano's postulates
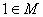
- If
, a unique 
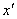different from 
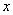exists, and 
- For
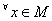, we have 
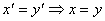
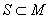
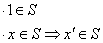
Then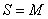
Definitions
Notation:
Let us denote 1' as 2, 2' as 3, 3' as 4, etc.
Sum
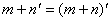
Multiplication
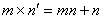
Properties
Commutative law
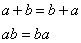
Associative law
Distributive law
Integer numbers
The set formed by natural numbers, 0, and negative natural numbers
··,-3,-2,-1,0,1,2,3,··
The result of a finite number of addition, subtraction, and multiplication operations among integer numbers is also an integer number.
Considering an integer number
and a natural number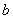 
, there exists only one pair of integer numbers 
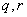satisfying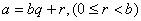
is divisible by 
is called a multiple of 
, and
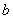is called an aliquot of 
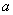.[0]Top