Orthogonal System
Orthogonality
Consider
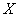: an inner product space and also a normed space with 
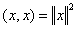for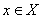 
.
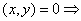
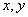are orthogonal.The inner product is a real number, and the angle
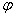formed by 
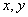is defined as
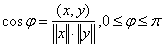,If the following holds for
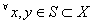
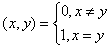
then
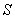is an orthonormal system.If the elements of
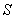can be arranged as a sequence, then 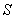is an orthonormal sequence.Fourier expansion
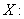inner product space
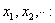finite or countable infinite orthonormal sequenceIf
,
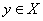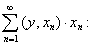Fourier series
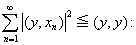Bessel's inequalityCompleteness
If
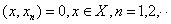, then 
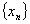is a complete sequence when 
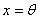.Linear combination field: the set of first-order, linear combinations of
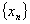
The three statements below are equivalent:
- The linear combination field of
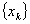is dense for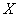 
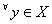
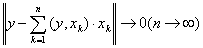
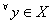
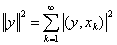
[0]Top