Overfield
If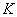
is a subfield of 
,
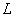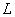is called an overfield of 
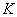.If
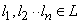are determined such that an arbitrary element 
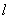of 
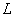can be expressed as a linear combination of 
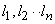as in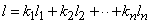
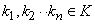
, then
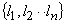is called a base.If
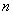is finite, then 
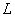is called an overfield of 
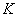.If
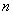is infinite, then
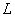is an infinite overfield of 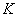.If a polynomial
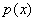with root 
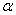exists in 
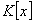with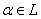 
, then 
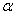is algebraic.If
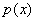is irreducible in 
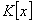, then
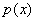is called a minimal polynomial.Consider
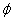as a mapping from the polynomial ring 
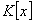to the subring 
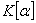of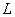 
.
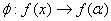
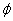is a surjection homomorphism mapping, and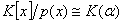
Consider that
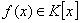.If
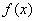can be decomposed into first-order factors in 
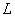, then 
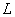is called a decomposition field of 
.
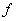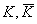:Fields
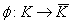:Isomorphism mappingIf
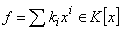, then the following expression is true: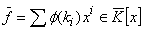
Consider that the decomposition field of
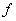is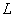 
, and the decomposition field of 
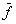is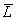 
.In this case, the isomorphism mapping
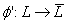resulting from the extension of 
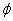exists.When all irreducible polynomials
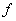of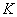 
have a single root, 
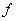is called to be separative on 
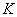.[0]Top