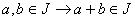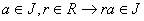Residue Ring,Homomorphism Mapping
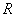:Ring
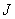:Subset of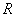 
When
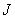is a left-ideal of 
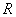, and a right-ideal if 
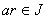. If both conditions are met, it is called ideal.
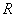:Ring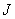
:Ideal of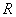 
A set of residue classes
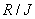with divisor 
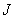is a residue class ring (quotient ring) if 
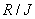is a ring on additive and multiplicative operations.
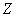:Rational integer ring
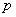:Prime number greater than or equal to 2Quotient ring
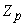is a field.
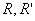:Ring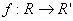
For
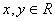, if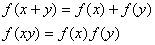
then
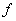is a homomorphism mapping.If an isomorphism mapping from
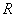to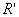 
exists, then 
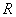and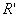 
are isomorphic.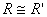
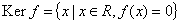
is the called kernel of
.
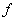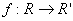:homomorphism mapping
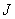:KernelIf the mapping
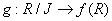generated from 
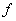is an isomorphism mapping.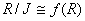
[0]Top