12/31/2007

Last time, by differentiating 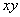, and then, by integrating it, we arrived at the next equation:


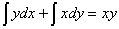
Well, now let's see what will come out in the case of differentiating it by n times, and then, integrating it by n times as well.
However, before we consider the case, we need to straighten out the problem of integral sign.
Although, we write 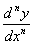when we differentiate 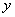by n times but we do not write 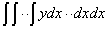when we integrate 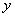by n times.
By differentiation, we mean to come down on the function indicating the gradient of tangent line, and the computational result of differentiation will necessarily be a function.
The integration 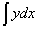expresses the square measure of functional intervals, and because 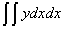has no geometric meaning, and, therefore, it could be deduced that 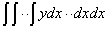neither has any geometric meaning.

Now, let's see what happens if we treat the computational result of integration as a function. Can't we not treat 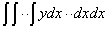as a function of having integrated n times?
In this case, it could be deduced that we can ignore the constant of integration. In this instance, because the opposite of differentiation is integration, we would like to express the case by below signs:
,
,
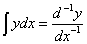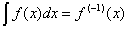
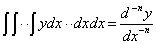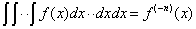
The Properties of equation:
,
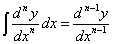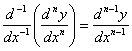
When we employ the above expression in an equation, we can conceive the Laurent expansion and express as .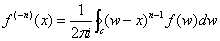

In the case of rational functions such as 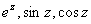, the coefficient of 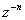is zero and, henceforth, we come to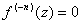
Why is it integration 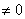in the ordinary interval (curve line)? Since it looks quite different from what we ordinarily know as integration, allow me to call it a "local integration".

When we ignore the coefficients, the differentiation would be


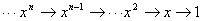
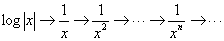
And the integration would be as follows:


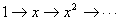
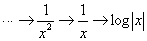
Although the opposite of differentiation is integration, the below cannot be tolerated:

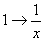
And the reason is because we suspect a flaw in:

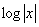
Conversely, could there be a deeper analytical meaning in ?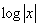

By the way, we know that differentiation is to determine tangent equation and integration is to determine area function but can't we express the determinations of tangent and area more purely in terms of geometric model?
Integration goes from lines to areas, and double integration moves further up in dimension to cubic volume. Does that mean differentiation is to go down in dimension?

If we differentiate 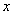in polar form in 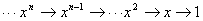, then, what will be the behavior of ?
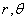Isn't it so that polar form and differential and integral calculus are put as unrelated even in books on function of complex variable?

Historically speaking, the definition of differential and integral calculus stemmed from its discovery by Newton and Leibniz. What could have happened if the development had stemmed from a different definition?

In phase analysis, differential and integral calculus is treated as an operator. Then, could 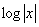be the singular point of an operator?

Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis|