Inference from relativity theory and expanding cosmology

This inference was made in my thirties and forties. It has never been reported or checked by any professor and nobody knowns if it is authentic.

Relativity theory tells that matter cannot move faster than speed of light.
According to some books on cosmology, the universe is constantly expanding and its expansion velocity "is proportioned to distance". The expansion means that of space, and the statement above does not always deny "Expansion velocity can become more than speed of light".

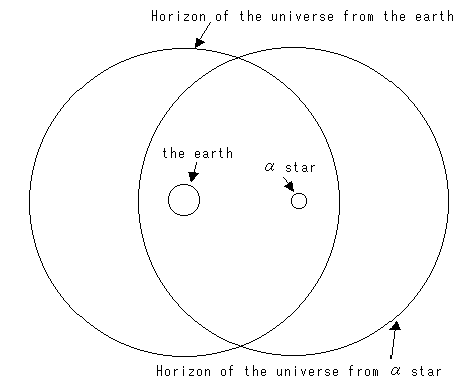
There is a boundary at which the recession velocity from the earth will become more than speed of light that is defined as horizon of the universe.
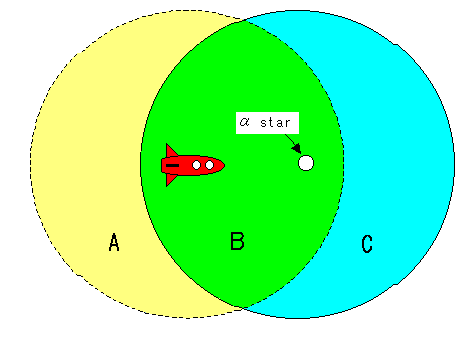
Now, suppose there is 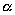star near the horizon. "People" of 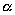star do not understand "we are at the verge of the universe". There ought to be a universe which can be seen from 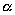star as well as a horizon of 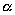star.

Suppose both the expansion velocity of the universe and velocities of moving matters are "absolute".
There is a rocket flying near the earth nearly at speed of light, and the rocket is flying toward 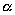star at the same speed as 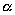star's recession velocity, then the universe as seen from inside the rocket is the same as that as seen from 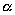star.
"A" domain becomes invisible from inside the rocket, and instead "C" domain ought to become visible.

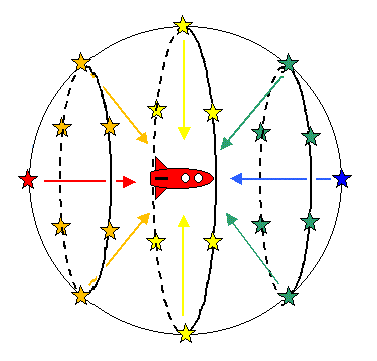
According to relative theory, "If a rocket flies nearly at speed of light, we can seen as if there were X-ray stars in the center of our flying direction and purple, blue and yellow stars around them due to aberration-of-light phenomenon and Doppler effect of light".

This is true only for "B" domain, and "C" domain subsequently becomes visible, which would allow these stars to converge frontward, but there ought not to be seen any color spectrum like a rainbow.

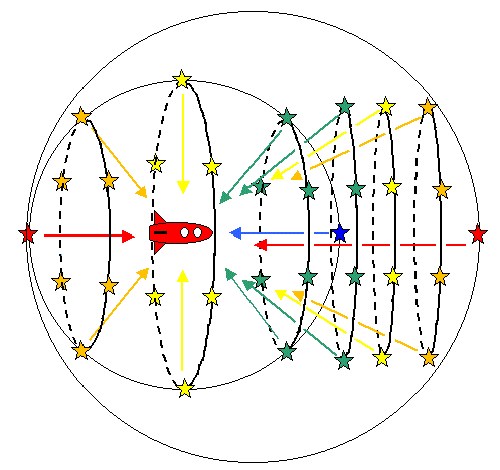
Now, if "C" domain can be seen from the rocket, vice verse from "C" domain there has to be a phenomenon "There can be seen a rocket flying near the earth, but not be seen the earth". This is likely to be a contradictory statement.

According to expansion universe theory, "The universe has its beginning, or big bang and is constantly expanding", and so the universe is not infinite, but finite.

Suppose there is 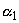star near a horizon of a universe as seen from 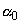star; 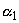star also has its horizon near which is 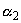star in the opposite direction of 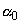; and so on.
Then, we get a stellar series: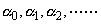

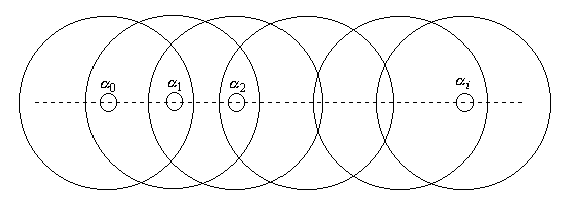
If the universe is infinite, any 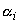star ought to be different from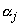 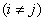star in this series.
If the universe is finite, some 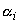star ought to be the same as .

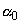If this is true, the following may occur.

• If travelling from the earth with a rocket having its speed beyond speed of light, we have to come across the earth on our travel.
• If a bullet can readily go beyond the horizon of the universe at its speed beyond speed of light when a man on the earth shoot a gun frontward, then the bullet has to come from behind him after a little while.