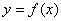 is a function defined on the
is a function defined on the 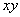 plane, I assume also that the function can be expressed with Taylor Series as follows.
plane, I assume also that the function can be expressed with Taylor Series as follows.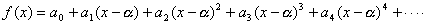
At this time, what is the necessary and sufficient condition for the intervals of
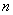 of the degree as expressed below ?
of the degree as expressed below ?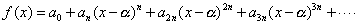
August 1999


I describe application from relation of integral to Taylor Series.
You may think this is not application, however. I had some doubt by chance from relation and I arrived finally here.
Although I proved, let me omit insertion of the proof.
Assuming that 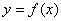 is a function defined on the
is a function defined on the 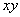 plane, I assume also that the function can be expressed with Taylor Series as follows.
plane, I assume also that the function can be expressed with Taylor Series as follows.
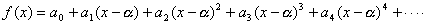
At this time, what is the necessary and sufficient condition for the intervals of 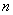 of the degree as expressed below ?
of the degree as expressed below ?
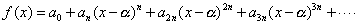
I generalize the interpretation of the variable of 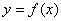 from real number
from real number 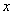 to complex number
to complex number 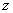 .
.
I convert 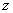 into the polar form and set
into the polar form and set 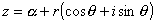 to obtain
to obtain 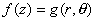 .
.
The necessary and sufficient condition for intervals of 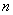 of the degree of
of the degree of 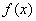 is that
is that 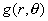 satisfies constantly the formula
satisfies constantly the formula 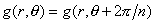 .
.
Consequently, if 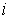 is not a multiple of
is not a multiple of 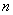 ,
, 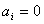 , and for a derivative of
, and for a derivative of 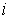 order of
order of 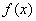 ,
, 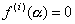
What is the value of 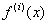 at
at 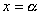 ?
?
Formerly, the result could not be found without calculation. Now, the result may be obtained clearly based on the periodicity of function.
We can see that there is rule in differential coefficient.
|
Total(1997) |
|
Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis| |