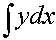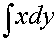
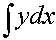Relationship between and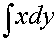

[Introduction]

I show the following formula that I discovered in May 1998. Although I wrote "discovered", this is a low level formula that I hit upon when I was lost in thought. I thought that there is some relationship about the sum of the integral of the function and the integral of its inverse function.
As a matter of course, I cannot write a paper based on this.
This formula is unnatural from a commonsense standpoint, but this is natural if we look at this carefully. The formula is attractive for this reason.
For making public of this formula, I have obtained consent of the professor.

[Formula]

Supposing that 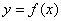is a function defined on the 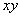plane, and differentiable, and not a constant, then
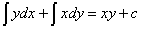(C:integration constant)

[Proof]

The proof is very easy.
Differentiate 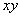with respect to 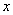and then integrate the result with respect to . (End of proof)

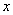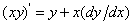
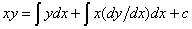
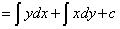
[Other]

Also we can get the formula 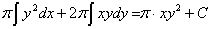from 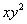, the formula 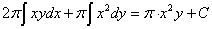from .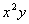

[History]

In March 1998, I hit on an idea.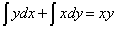 may be true.
However, for example, about an algebraic equation of high degree,
since
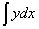is a computable formula,
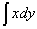is an incomputablke formula, and
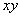is a computable formula,
therefore, the equation (computable formula)+(incomputablke formula)=(computable formula) holds, indicating irrationality.

In May 1998, I tried to calculate actually using a simple function and I found that the equation held by chance. I thought by intuition that the equation 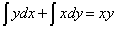held.
I proved it several days later. When I completed the proof, I found that 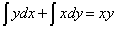is application of integration by parts. Therefore the emotion of the discovery was reduced by half.
However, I am impressed by the discovery that the relationship between the integral of a function and the integral of its inverse function is expressed by a linear formula.
Finally, I think 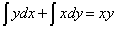is a formula like Columbus'egg.

Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis|