I will use an equation well known to you all. That is:
"Velocity (Speed) = Distance (Length) / Time"
You must have learned it in your physics class.

When the velocity is constant and close to the speed of light, as mentioned before, I explained that "the scale of time" is different. In case "velocity" is fixed, then the interpretation of "distance (length)" must change.

Say that 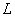stands for length for a person who is physically active and 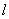stands for length for a person who remains stationary.
I will try to come up with an equation that converts 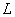into .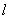

   

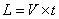
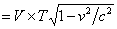
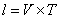
Therefore:


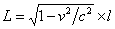
[Thought Experiment]

Let's suppose that a train travels at close to the speed of light makes a uniform motion for the length of one passenger coach.

Moreover, let's suppose the time is thrice slower in comparison with that of outside the train. I shall examine how the train would look in case the time is thrice slower.

First of all, if the train would appear like the diagram below indicates, then, the velocity simply became 1/3, and, therefore, it is absolutely unlikely.
If the scale of length becomes 1/3 as the diagram below indicates, then, it satisfies the first formula.

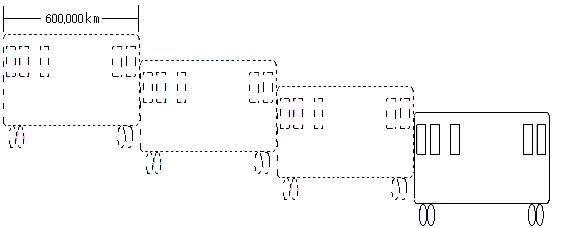
This means that the length of an object traveling at the speed of light would appear to be shorter. However, if one looks at the ground from an object traveling at the speed of light, then, objects on the ground would appear to be shorter.

Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis|