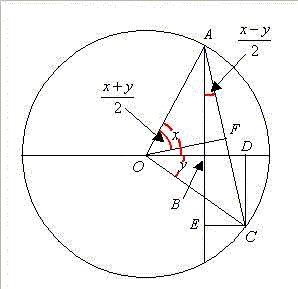
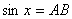
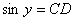
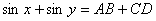
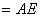
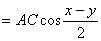
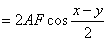
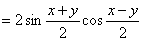
In this equation, let
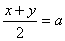 ,
,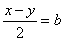 then, we get:
then, we get: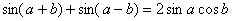
Thereafter, this equation was widely used in Europe as a method to simplify multiplication in the field of astronomical calculations.

 It could be the world's oldest relation between the sum and product of trigonometric function.
It could be the world's oldest relation between the sum and product of trigonometric function.
In the 16th century Europe, when decimal point has yet to be developed, Viete(1540-1603) tried to examine trigonometric function analytically.

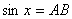
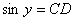
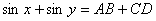
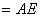
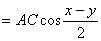
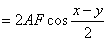
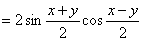
In this equation, let 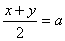 ,
,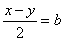 then, we get:
then, we get:
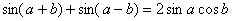
Thereafter, this equation was widely used in Europe as a method to simplify multiplication in the field of astronomical calculations.
For instance, say 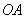 is 10,000, and prepare respective angular representation tables for the case of changing
is 10,000, and prepare respective angular representation tables for the case of changing 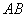 from 1 to 10,000, and changing
from 1 to 10,000, and changing 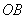 from 1 to 10,000 as well. For angular measures, a sexagesimal system of angular measure (Examples: 98°25´40´´) must have been used, but we shall employ a sexagesimal system of angular measure inclusive of decimal point(Example: 98´.427777). In Europe those days, tables up to 12 digits and 15 digits existed.
from 1 to 10,000 as well. For angular measures, a sexagesimal system of angular measure (Examples: 98°25´40´´) must have been used, but we shall employ a sexagesimal system of angular measure inclusive of decimal point(Example: 98´.427777). In Europe those days, tables up to 12 digits and 15 digits existed.
Let's calculate 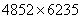 as an example.
as an example.
From the table, let's find angle 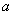 that makes
that makes 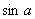 equal to 4852 and angle
equal to 4852 and angle 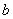 that makes
that makes 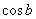 equal to 6235. Then, calculate as below:
equal to 6235. Then, calculate as below:
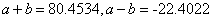
Look for 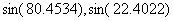 in the table. If there no exact values are found, and then use those values that are near.
in the table. If there no exact values are found, and then use those values that are near.
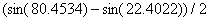
This gives us the value of: 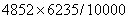
Soon after this, because both Napier (1550-1617) and Briggs (1561-1630) invented common logarithm applicable to multiplication and division, this method was ceased to be used.
Corresponding Table
| sin | angle | cos | angle |
| 1 | 0.005729578 | 1 | 89.99427042 |
| 2 | 0.011459156 | 2 | 89.98854084 |
| 3 | 0.017188734 | 3 | 89.98281127 |
| 4 | 0.022918312 | 4 | 89.97708169 |
| 5 | 0.028647891 | 5 | 89.97135211 |
| 6 | 0.03437747 | 6 | 89.96562253 |
| 7 | 0.040107049 | 7 | 89.95989295 |
| 8 | 0.045836628 | 8 | 89.95416337 |
| 9 | 0.051566209 | 9 | 89.94843379 |
| 10 | 0.057295789 | 10 | 89.94270421 |
| 11 | 0.06302537 | 11 | 89.93697463 |
| 12 | 0.068754952 | 12 | 89.93124505 |
| 13 | 0.074484534 | 13 | 89.92551547 |
| 14 | 0.080214118 | 14 | 89.91978588 |
| 4852 | 29.02557669 | ||
| 6235 | 51.42782406 | ||
| 9990 | 87.43744127 | 9990 | 2.562558733 |
| 9991 | 87.5689636 | 9991 | 2.431036405 |
| 9992 | 87.708016 | 9992 | 2.291983997 |
| 9993 | 87.85606316 | 9993 | 2.143936842 |
| 9994 | 88.01511672 | 9994 | 1.984883276 |
| 9995 | 88.18807286 | 9995 | 1.811927138 |
| 9996 | 88.37937661 | 9996 | 1.620623393 |
| 9997 | 88.59651067 | 9997 | 1.403489331 |
| 9998 | 88.85406531 | 9998 | 1.14593469 |
| 9999 | 89.18970856 | 9999 | 0.810291437 |
|
Total(1997) |
|
Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis| |