Pythagoras happened to cut off the paving stones as shown in
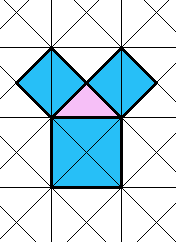
so causing his idea to be developed into the theorem


[Introduction]
Pythagorean theorem was found around in B.C. 570. It was only known to great scientists at that time, leading to be what can be understood by junior-high-school students now.
[How was the theorem found?]
There are two propositions about how the theorem was found:
(1) Seeing the stone pavement in some temple,

Pythagoras happened to cut off the paving stones as shown in

so causing his idea to be developed into the theorem
(2) Among the ancient Egyptian knowledge was an old theorem that if a right
triangle has its three edges a, b, and c whose ratio is 3:4:5, then there
stands an equation 32+42=52.
Among the ancient Babylonian knowledge was another old theorem that if a right triangle has its three edges a, b, and c whose ratio is 5:12:13, then there stands an equation 52+122=132.
Such knowledge put together had been developed into the Pythagorean theorem.
I stand for the proposition (1).
[Inside story]
The Pythagorean schools in those days were in a closed system, but not like our schools now.
Those students had to keep what was taught inside the school to themselves and prohibited from their publishing under their personal names whatever they originally found.
Accordingly, it is still unknown whether or not this Pythagorean theorem (so-called theorem of three squares) was found by Pythagoras himself.
|
Total(1997) |
|
Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis| |