Infinity



I state my conclusion first that there are two kinds of infinite of potency of countable set and property of continuity.
[Potency]
Potency means the number of elements of infinite set, which is an extended concept of the number of finite set.
[Potency of countable set]
When primitively counting the number of elements of set, we chant or breathe
1, 2, 3, ---. Therefore, the element of finite set is one-to-one correspondent to a set of natural numbers {1, 2, 3, ---,n}.
Among infinite sets, a set equivalent (, or one-to-one correspondent) to a set of natural numbers is defined as a countable set. The number of these elements is defined as potency of countable set and represented by a sign  (aleph zero).
(aleph zero).
Examples of countable set
(1) set of natural even numbers
A set of natural even numbers {2, 4, 6, 8, ---} is allowed to correspond
to a set {1, 2, 3, 4, ---}. Therefore, a set of even numbers is a countable
set. In the same way, a set of odd numbers is a countable set.
{set of even numbers} U {set of odd numbers} = {set of natural numbers}
then
 +
+ =
=
However, the following subtraction  =0 does not hold, upon subtracting
=0 does not hold, upon subtracting  from either.
from either.
(2) set of positive rational numbers
Since rational numbers are represented by p/q (where p and q is natural numbers), p and q are successfully allowed to become one-to-one correspondent to natural numbers in the order of numerator p and denominator q.
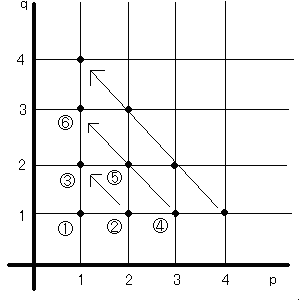
Therefore, a set of rational numbers is a countable set. This leads to
 *
* =
=
However, the following division  =1 does not hold, upon dividing either member by
=1 does not hold, upon dividing either member by  .
.
[Potency of continuity]
In the case of a set of real number [X: 0<X<1]
First, let A=5 and B=6, for example, 0.56 is to be represented by 0.AB.
If a countable set, then a set of real number has to be X1, X2, X3, X4,--- by arranging them in a row.
Suppose the n'th real number among them is Xn=0. An1An2An3An4---,and arrange them in ascending order from X1,
w1OD`11`12`13`14---
w2OD`21`22`23`24---
w3OD`31`32`33`34---
w4OD`41`42`43`44---
·
·
·
Focusing our attention on the diagonal figures and assuming Bn=1 for Ann as an even number and Bn=2 for Ann as an odd number.
Suppose a number of Y: Y=0. B1B2B3B4----- then, Y is not equal to any Xn.
In other words, there is at least one element in real number such as cannot be arranged if done as a countable set.
Thus, real number is not countable. Real number is Potency of continuity and represented by a sign 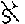 (aleph).
(aleph).
This proof method is referred to as Diagonal method.
If naturally fairly taken in, you cannot apply this line of argument to rational number either
For example, a rational number 1/7=0.142857142857142857----- will be a repeating decimal by a unit of 142857.
Generally, if a rational number p/q is an infinite decimal having its decimal part repeated infinitely, that decimal never fails to repeat (I recommend you to prove this because it is easy).
Then, if we create another number Y such as Y=0. 1211221211121211122222--- 1 and 2 recurs randomly so failing to be a rational number.
[Relationship between  and
and 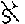 ]
]
2
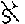 (2 to the
(2 to the  =
=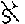 )
)
 (aleph zero).
(aleph zero). +
+ =
=
 =0 does not hold, upon subtracting
=0 does not hold, upon subtracting  from either.
from either.
 *
* =
=
 =1 does not hold, upon dividing either member by
=1 does not hold, upon dividing either member by  .
.


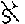 (aleph).
(aleph).