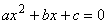
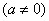
has its general solution:
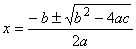


I would like you to know general solution of algebra equation and abstract mathematics.
[Quadratic Equation]
The quadratic equation:
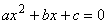
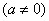
has its general solution:
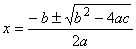
[Cubic Eqaution]
To solve a general solution of the cubic equation:
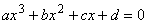
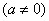
upon assuming
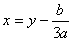 ,
,
it leads to
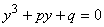
This equation can be solved.
Upon assuming using 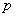 and
and 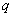 , and multiplying this by cubic root
, and multiplying this by cubic root 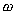 , it reduces to
, it reduces to
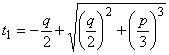
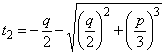 .
.
After selecting one either from 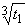 ,
, 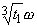 ,
, 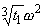 or from
or from 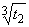 ,
, 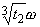 ,
, 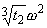 ,
the product satisfying
,
the product satisfying 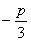 is assumed again as:
is assumed again as: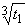 ,
,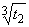 .
.
Then, we have as general solutions of the cubic equation:
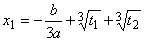
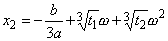
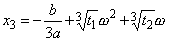
This solutin is termed Cardano's solution.
[Quartic Equaiton]
There is some method to solve its general solutions, and check it by yourself.
[not less than Quintic Equations]
There is no expression to solve their general solutions.
[History]
It is Abel and Galois that first demonstrated that not less than quintic equations have no general solutions of their own.
Abel and Galois did not compete for this demonstration in studying, but could independently demonstrate without knowing each other.
Abel created field theory to demonstrate that algebraic solution of not less than quintic equations is inconsistent.
Galois created group theory to demonstrate such inconsistency by solving necessary and sufficient condition on which algebraic solution is feasible.
It may safely be said that abstract mathematics began with such demonstrations by two mathematics masters.
[To Senior-high-school students]
The solutions of Cubic and quartic equations are contained in technical books, so you can check to understand.
Yet, you will not learn them in any mathematics department in university: "Learn by yourself !"
However, you can learn in algebraic lectures the theory that not less than quintic equations have no general solutions as well as the necessary and sufficient condition for algebraic solvability.
[In conclusion]
I here list definitions of group. In addition, I have forgotten all about group including them and extracted from some technical books.
Definitions of ring and field will come after those of group, please check by yourself.
We assume that Group 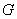 is not an empty set and a mapping for
is not an empty set and a mapping for 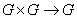 is given.
is given.
An element 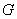 corresponding to an element
corresponding to an element 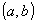 from
from 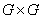 is to be described as
is to be described as 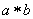 .
.
Then, 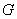 is referred to as with respect to law of composition
is referred to as with respect to law of composition 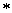 if the following three conditions are satisfied:
if the following three conditions are satisfied:
1. for every element  from
from 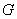 ,
,
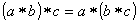
2. for every element 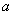 under the condition that
under the condition that 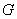 has one element
has one element 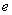 ,
,
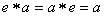
3. for a given element 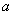 , there is such an element
, there is such an element 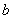 in
in 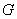 that satisfies:
that satisfies:
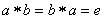
"1." is termed associative law, e in "2." as identity element, and b in "3." inverse element.
|
Total(1997) |
|
Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis| |