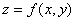 will generate a surface in three-dimensional space. Differentiating the function with respect to
will generate a surface in three-dimensional space. Differentiating the function with respect to 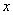 or
or 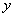 is termed partial differentiation and described as:
is termed partial differentiation and described as: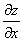
Naturally, there is also partial differential equation" like differential equation.


I would like to explain to you additional types of differential and integral calculus for mathematics in university. To explain them, there are needed strict and exact conditions for the function, and yet I will only use the expression smooth functions so that senior-high-school students can also understand my explanation.
[Partial differentiation]
A function of two variables 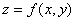 will generate a surface in three-dimensional space. Differentiating the function with respect to
will generate a surface in three-dimensional space. Differentiating the function with respect to 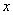 or
or 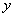 is termed partial differentiation and described as:
is termed partial differentiation and described as:
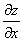
Naturally, there is also partial differential equation" like differential equation.
[Implicit Function]
If there is a relation 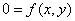 , then there is also a function
, then there is also a function 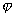 satisfying
satisfying 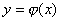 and
and 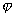 is termed implicit function. Then, the following equation stands:
is termed implicit function. Then, the following equation stands:
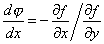
[Multiple Integral]
Integrating 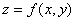 with respect to a domain
with respect to a domain  in a plain
in a plain 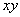 is termed multiple integral and described as:
is termed multiple integral and described as:
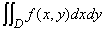
The domain 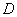 means various shapes including rectangle, circle, triangle, a domain bounded by two functions
means various shapes including rectangle, circle, triangle, a domain bounded by two functions 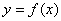 and
and 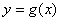
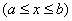 .
.
For example, let 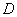 is generated by satisfying
is generated by satisfying 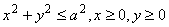 : then
: then
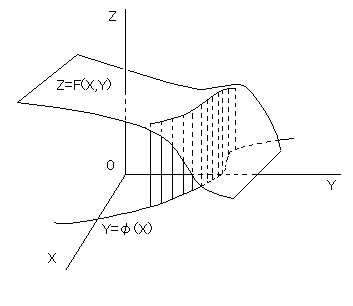
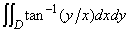 represents a volume of the domain bounded by the lines in the figure below.
represents a volume of the domain bounded by the lines in the figure below.
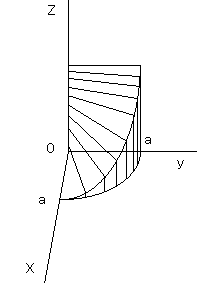
[Curvilinear Integral]
Integrating Surface 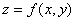 in three-dimensional space along Smooth curve
in three-dimensional space along Smooth curve 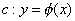 is termed curvilinear integral and described as:
is termed curvilinear integral and described as:
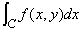
It means solving the area of the domain as illustrated in the figure below.
[Complex Integral]
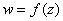 is assumed as a function from a complex number
is assumed as a function from a complex number 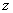 to a complex number
to a complex number 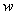 . Complex integral is like curvilinear integral, integrating
. Complex integral is like curvilinear integral, integrating 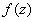 on a curve assuming Curve
on a curve assuming Curve 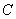 in
in 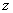 plain. It is described as:
plain. It is described as:
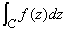
Complex integral has relatively different characters from real integral.
[Lebesgue Integral]
This means integrating 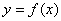 under the consideration that
under the consideration that 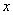 is a set. Lebesgue Integral defines integral without a concept of differentiation, while a condition
of differentiable is needed for Riemann Integral as above-mentioned up to Complex Integral. For example, Lebesgue Integral is used to strictly treat of probability
that will never permit smooth treatment.
is a set. Lebesgue Integral defines integral without a concept of differentiation, while a condition
of differentiable is needed for Riemann Integral as above-mentioned up to Complex Integral. For example, Lebesgue Integral is used to strictly treat of probability
that will never permit smooth treatment.
|
Total(1997) |
|
Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis| |