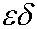 (epsilon-delta) technique
(epsilon-delta) technique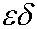 (epsilon-delta) technique
(epsilon-delta) technique

If we have a function 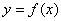 in
in 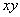 plane, then a differential coefficient with respect to
plane, then a differential coefficient with respect to 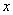 is to be defined as:
is to be defined as:
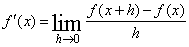
Now, 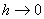 in the expression above means "allow
in the expression above means "allow 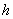 to approach but not equalize to 0."
to approach but not equalize to 0."
Put 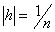 (
(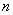 is a natural number) : then
is a natural number) : then
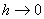 is equivalent to
is equivalent to 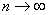 .
.
Now I will explain about  . We can conceptually understand "natural numbers is an infinite set," and still it is practically impossible to "list every natural number." In other words,
. We can conceptually understand "natural numbers is an infinite set," and still it is practically impossible to "list every natural number." In other words, 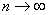 can be explained only philosophically. The same is the case with
can be explained only philosophically. The same is the case with 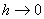 .
.
Accordingly, there was introduced 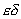 technique that requires mathematical strictness and does not use "infinite".
technique that requires mathematical strictness and does not use "infinite".
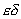 technique uses the expression:
technique uses the expression:
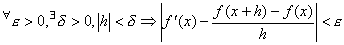
that has the wording "for every 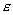 > 0, there exists a
> 0, there exists a 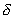 > 0,such that : if
> 0,such that : if 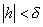 , then
, then 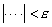 ".
".
Next, I will describe the meaning of 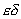 technique. To describe briefly, take the following meaning of "A function
technique. To describe briefly, take the following meaning of "A function 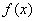 is continuous":
is continuous":
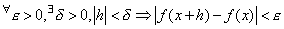
The expression above can be illustrated as follows:
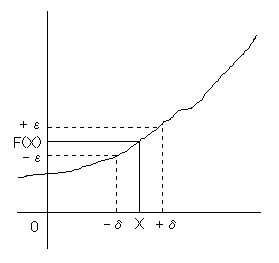
"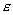 " as in "for every
" as in "for every 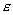 " may be either
" may be either 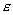 =600 or
=600 or 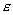 =2 and typically means very small or infinitesimal values such as
=2 and typically means very small or infinitesimal values such as 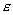 =0.0013 and
=0.0013 and 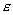 =10-23. "there exists a
=10-23. "there exists a 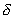 " means that there is an "
" means that there is an "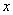 " range
" range 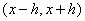 such that satisfies "
such that satisfies "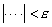 " and that
" and that 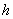 satisfies
satisfies 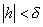 .
.
For example, Function 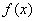 is discontinuous at a point
is discontinuous at a point 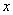 as shown in the following figure:
as shown in the following figure:
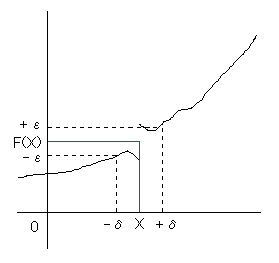
For a substantially small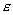 there exists no
there exists no 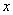 such that satisfies
such that satisfies 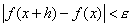 near
near 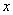 in range
in range 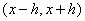 , so we cannot define
, so we cannot define 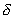 .
.
|
Total(1997) |
|
Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis| |