

Torricelli / Infinitesimal geometry
Torricelli(1608-1647) had contributed to development of mathematics, physics, optics, dynamics, ballistics and meteorology. Among them, he is especially famous in 'Torricelli's experiment' that created the first vacuum of human beings.
A basic concept of Torricelli is a "non-separable method". He improved the method for application to some curves and curved surfaces.
[Area of circle]
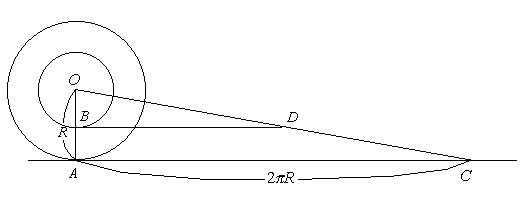
Let 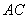 represent a straight line that equals to length of the circle of radius
represent a straight line that equals to length of the circle of radius 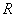 . We draw a circle having a radius
. We draw a circle having a radius  at a center
at a center 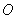 , passing a point
, passing a point 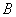 on the radius
on the radius 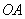 . We also draw a straight line
. We also draw a straight line 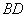 in parallel with
in parallel with 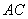 .
.
Length of a line segment 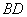 equals to that of a circle of radius
equals to that of a circle of radius 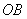 as triangles
as triangles 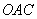 and
and 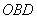 is similar.
is similar.
A set of non-separable circles corresponds to a set of non-separable triangles. Areas of the circles equal to those of the respective triables.
Therefore, 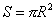 .
.
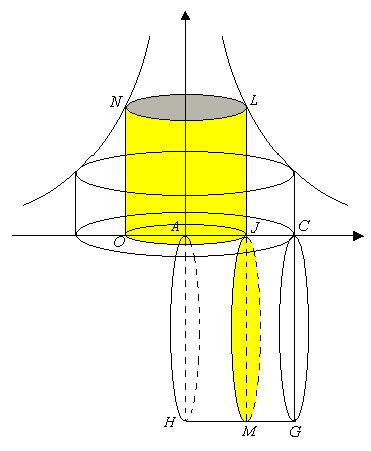
[Sharp-pointed body of hyperboloid]
Volume of an infinitely extended solid is calculated below. The volume is that of a body of rotation with a center on 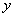 axis of a hyperbolic curve
axis of a hyperbolic curve 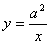 . That can be expressed as
. That can be expressed as 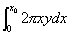 .
.
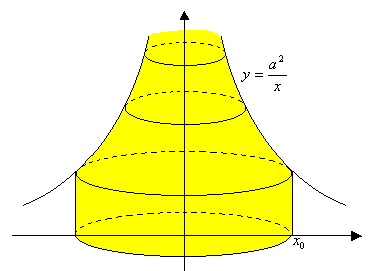
As seen from the figure above, a figure extending infinitely has finite volume. This is the first discovery at the time of Torricelli. He showed that the non-separable amount of the solid was formed of surface of a circular cylinder 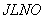 having sides
having sides 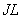 .
.
Let surface area of the circular cylinder 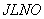 be
be 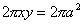 , length of the diameter
, length of the diameter 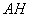 of the bottom of the circular cylinder
of the bottom of the circular cylinder 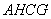 be
be 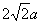 , and height
, and height 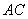 be
be 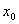 .
.
Area of the circle of the diameter 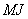 in the circular cylinder
in the circular cylinder 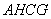 equals to surface area of the circular cylinder
equals to surface area of the circular cylinder 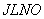 . Therefore, area of the sharp-pointed hyperboloid body equals to non-separable area of the circular cylinder
. Therefore, area of the sharp-pointed hyperboloid body equals to non-separable area of the circular cylinder 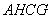 . Volume of the sharp-pointed body of hyperboloid equals to that of the circular cylinder
. Volume of the sharp-pointed body of hyperboloid equals to that of the circular cylinder 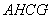 .
.

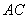 represent a straight line that equals to length of the circle of radius
represent a straight line that equals to length of the circle of radius 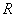 . We draw a circle having a radius
. We draw a circle having a radius 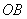 at a center
at a center 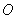 , passing a point
, passing a point 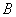 on the radius
on the radius 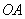 . We also draw a straight line
. We also draw a straight line 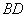 in parallel with
in parallel with 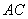 .
.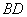 equals to that of a circle of radius
equals to that of a circle of radius 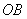 as triangles
as triangles 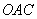 and
and 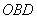 is similar.
is similar.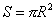 .
.


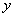 axis of a hyperbolic curve
axis of a hyperbolic curve 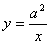 . That can be expressed as
. That can be expressed as 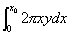 .
.
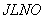 having sides
having sides 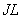 .
.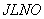 be
be 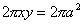 , length of the diameter
, length of the diameter 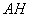 of the bottom of the circular cylinder
of the bottom of the circular cylinder 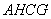 be
be 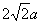 , and height
, and height 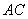 be
be 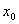 .
.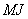 in the circular cylinder
in the circular cylinder 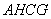 equals to surface area of the circular cylinder
equals to surface area of the circular cylinder 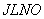 . Therefore, area of the sharp-pointed hyperboloid body equals to non-separable area of the circular cylinder
. Therefore, area of the sharp-pointed hyperboloid body equals to non-separable area of the circular cylinder 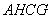 . Volume of the sharp-pointed body of hyperboloid equals to that of the circular cylinder
. Volume of the sharp-pointed body of hyperboloid equals to that of the circular cylinder 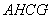 .
. 