Roberval / Infinitesimal Geometry

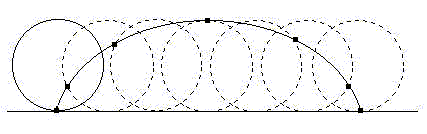
Roberval (1602-1675) studied algebra, geometry, dynamics and astronomy. With respect to differential and integral calculus, he studied cycloid that was in vogue at that point in time. Cycloid means the locus of the points on circumference of a circle rolling on a straight line.

[Tangent]

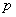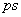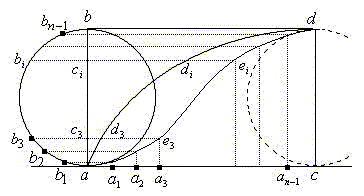
The movement of point is determined by the parallel motion and rotational motion. The component of parallel motion is depicted as and the same for rotational motion is depicted as 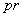. Since their respective sizes are the same, the angle bisector 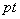will be the tangent of cycloid.

[Area]

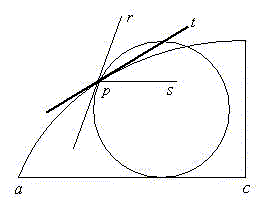
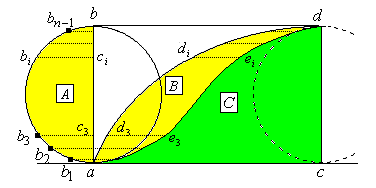
Roberval used non-separability to calculate the superficial content of the area surrounded by straight lines and cycloid.

Let 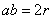, then .
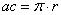The next step is to equally divide semi-circle 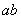and segment 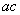by 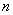that leads to the following ,.

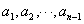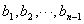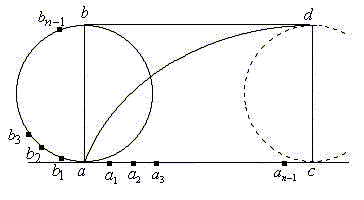
Draw a strait line horizontally from 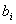, and, in this case, 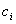is defined as the intersecting point with 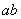and 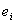is defined as the intersecting point on the vertical line drawn from 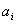. Then, the length of the segment could be expressed as 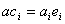. The locus of 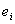will be a 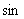curve.
Here, we should examine the locus of point 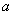. When the circle rotates and advances to point 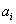then point 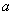comes to the position of point 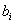. Let a point 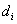to the left of 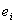that will be equal in length to that of 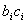. This point 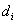will be defined as the position of point 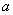where the circle verges at point 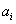. The locus of 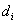will then becomes a cycloid.

Since the 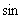curve equally divides the rectangle 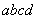, we have 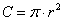and, in 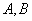, the length of 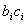is equal to length of 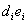, it becomes non-separable , then .

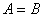Therefore,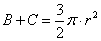

Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis|