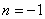Gregory / integration of hyperbola

In his treatise entitled "Opus geometri-cum quadraterae circuli et sectionum coni", Gregory (1584 - 1667) had successfully computed the case of , which Fermat was unable to calculate.
The computation was that he plotted points along the 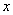axis in such a way that the length from 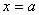increased in equal ratio and he drew vertical lines to 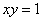(hyperbola) from the respective points; in this case, the superficial contents of the segments separated by vertical lines were in arithmetical progression.
However, I don't know this proof.

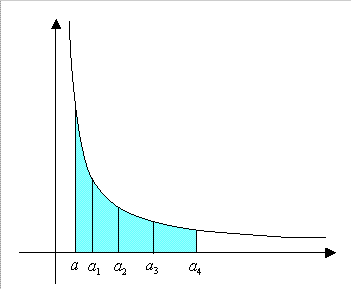
The property of the superficial content is expressed below in a typical mathematical expression of our own time.
Let 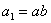, and make it the first term of the geometric progression.
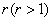is taken as the common ratio so as to lead to .

              
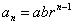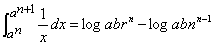
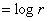
Therefore, the interval is in geometric progression but the superficial content is in arithmetical progression.

Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis|