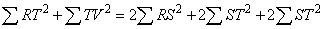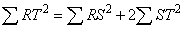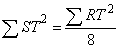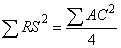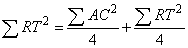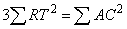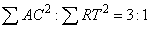Cavalieri / Infinitesimal geometry
Cavalieri(1598-1647) sought the general solution for solving the areas/volumes rather than the specific solution of quadrature by parts.
The fundamental concept in Cavalieri's geometry is referred to as "non-separability". This concept states that, for example, when examining a type of plane figure whose boundary does not intersect with a given line at not less than two points, we are to divide it by the parallel ruling in the plane or its divided sections are non-separable.
Speaking plainly, this idea is that moving of a point will generate a curve, line segments will generate a plane figure, and planes will generate a solid.
[parallelogram]
If diagonal BD is drawn in parallelogram ABCD, then an area of this parallelogram become twice as large as that of either triangle formed by the diagonal.
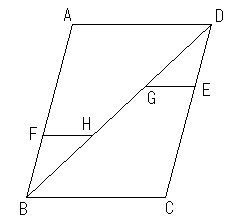
Set points E and F as satisfying DE=BF. Draw lines parallel to side BC at the points E and F, and their points of intersection with the diagonal are defined as G and H respectively. In length, there results EG=FH. Therefore, the segments put together for 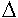 ACD is equal to those put together for
ACD is equal to those put together for 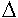 BCD. Hence, in area there results
BCD. Hence, in area there results 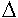 ACD=
ACD=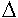 BCD. In addition, since the segments put together for the parallelogram become twice as large as that of the segments put together for either triangle, the area of this parallelogram becomes twice as large as that of either triangle.
BCD. In addition, since the segments put together for the parallelogram become twice as large as that of the segments put together for either triangle, the area of this parallelogram becomes twice as large as that of either triangle.
[Power]
Suppose there are two prisms 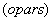 and
and 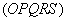 each having a square as its basal plane and they are similar.
each having a square as its basal plane and they are similar.
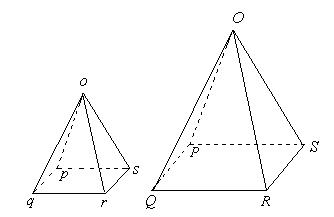
Let Volume of Prism 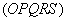 =
=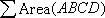
then from their similarity,
Volume of Prism  :Volume of Prism
:Volume of Prism =
=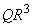 :
: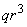
Area of Square 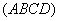 : Area of Square
: Area of Square 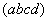 =
= 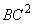 :
: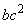
Therefore,
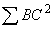 :
: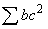 =
=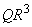 :
: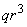
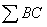 :
: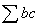 =
=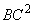 :
: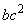
[Cavalieri's Principle]
If a third parallel line 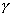 that is produced in parallel with base line
that is produced in parallel with base line 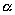 at domains
at domains 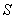 and
and 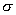 each generated by two parallel lines
each generated by two parallel lines 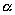 and
and 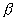 , always cut from these domains line segments
, always cut from these domains line segments 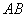 and
and 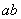 both of which are identical in length, then area
both of which are identical in length, then area 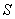 is identical with area
is identical with area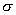 .
.
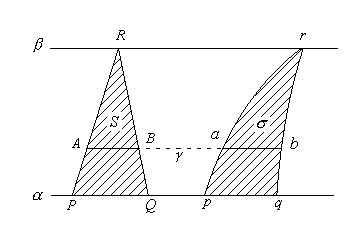
[Volume ratio of pyramid]
Let 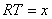 ,
,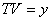 ,
,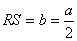 ,and
,and 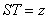 then,
then,
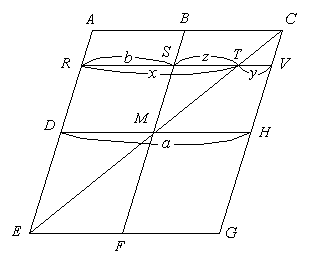
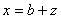
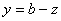
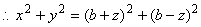
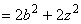
If line  is moved from
is moved from  to
to 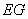 , then
, then
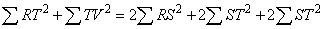
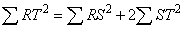
Taking into account that the volume ration of two similar patterns varies as the cube of ratio between the corresponding edges,
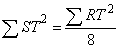
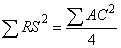
Therefore,
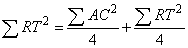
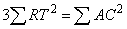
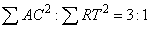
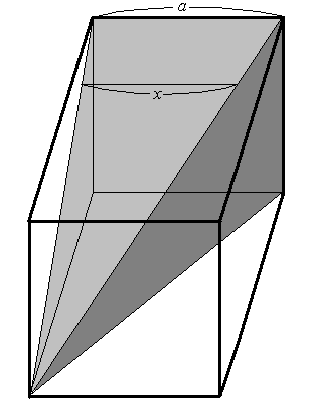
[Generalized power and Other patterns]
In Introduction for 4th experiment from Six geometric experiments published in Bologna in 1647, there was written as to two similar patterns using the power
of natural numbers beginning with 1, there was shown that the ratio between
their line segments as a whole is 2 : 1, the ration between their squares
as a whole is 3 : 1, the ration between their cubes as a whole is 4 : 1,
the ration between their quartics as a whole is 5 : 1 , the ratio between
those involved to 5th power as a whole is 6 : 1, the ratio between those
involved to 6th power as a whole is 7 : 1, and so on.
He calculated volumes of not less than 20 solids introduced by Kepler, areas of patterns consisting of Archimedean spirals and circles.

 ACD is equal to those put together for
ACD is equal to those put together for  BCD. Hence, in area there results
BCD. Hence, in area there results  ACD=
ACD=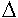 BCD. In addition, since the segments put together for the parallelogram become twice as large as that of the segments put together for either triangle, the area of this parallelogram becomes twice as large as that of either triangle.
BCD. In addition, since the segments put together for the parallelogram become twice as large as that of the segments put together for either triangle, the area of this parallelogram becomes twice as large as that of either triangle.

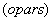 and
and 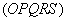 each having a square as its basal plane and they are similar.
each having a square as its basal plane and they are similar.
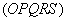 =
=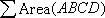
 :Volume of Prism
:Volume of Prism =
=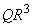 :
: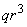
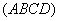 : Area of Square
: Area of Square 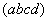 =
= 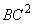 :
: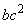
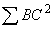 :
: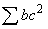 =
=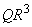 :
: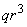
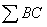 :
: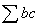 =
=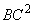 :
: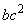
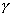 that is produced in parallel with base line
that is produced in parallel with base line 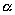 at domains
at domains 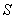 and
and 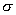 each generated by two parallel lines
each generated by two parallel lines 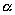 and
and 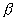 , always cut from these domains line segments
, always cut from these domains line segments 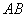 and
and 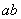 both of which are identical in length, then area
both of which are identical in length, then area 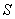 is identical with area
is identical with area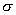 .
. 
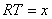 ,
,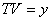 ,
,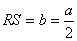 ,and
,and 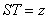 then,
then,
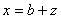
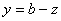
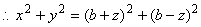
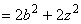
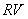 is moved from
is moved from 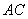 to
to 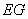 , then
, then