


Barrow / Calculus
Barrow (1630-1677) had made the great achievements in optics/mathematics by publishing Lectiones Opticae in 1669 and Lectiones Geometriae in 1670. Lectiones Geometriae contained a section explaining that the calculations of tangential method and quadrature method are reversed.
[The Definition of Tangent]
There is a point on a straight line shared with a curved line and all the points on a straight line close enough to that point are on the same side of the curved line.

[Finding Tangents]
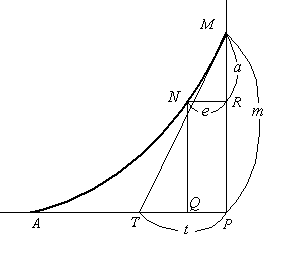
Draw a line of tangency at the point 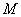 on the curved line
on the curved line 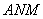 and call the point of intersection with a straight line
and call the point of intersection with a straight line 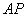 a
a 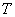 , and find the length of the straight line
, and find the length of the straight line 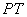 .
.
Let the arc 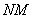 shall be infinitely small, draw
shall be infinitely small, draw 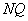 parallel to
parallel to 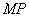 , draw
, draw 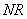 parallel to
parallel to 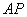 . Let
. Let 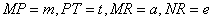 .
.
Then
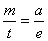
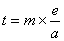
When 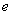 approaches 0, then the position of point
approaches 0, then the position of point 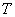 could be calculated.
could be calculated.
This calculation should comply with the stated rules below:
(1)Exclude the term that contains the power of 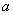 or
or 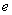 , and its product.
, and its product.
(2)Exclude the term that does not contain 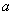 or
or 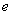 .
.
(3)Substitute 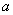 for
for 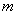 , and
, and 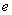 for
for 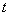 .
.
(Example)
Draw a line of tangency like: 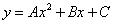
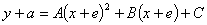
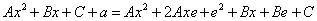
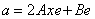
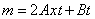
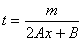
[Calculating the area]
A curved line 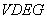 (function
(function 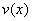 )bearing away from axis
)bearing away from axis 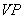 is given.
is given.
(Note)
Pay strict attention because it is different from the present system of coordinates. It is not minus (negative) just because function 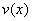 is subjacent to axis
is subjacent to axis 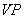 .
.
Constant number 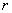 is introduced in order to adjust the dimension.
is introduced in order to adjust the dimension.
Draw curved lines that satisfy the conditions below:
The area of 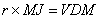
The area of 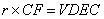
The area of 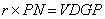
And then plot a point 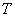 on
on 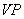 that makes the area of
that makes the area of 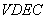 =
=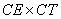 .
.
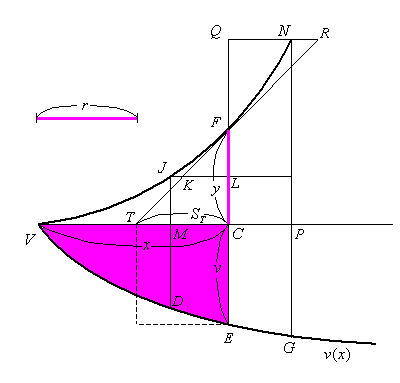
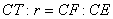
Due to these conditions, the straight line 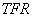 is now a tangent at point
is now a tangent at point 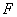 . (Proof is omitted)
. (Proof is omitted)
Let 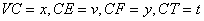 ,
,
then, the area of 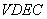
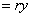 ----- (1)
----- (1)
Due to the property of tangent,
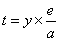
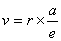
In modern expression, it becomes:
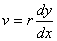 ----- (2)
----- (2)
From the above (1) and (2), it becomes obvious that the calculations to find the tangent and area are reversed.
|
Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis| |