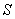 of a parabola
of a parabola 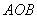 is 4/3 times as large as an area of
is 4/3 times as large as an area of 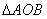 .
.


Archimedes / Quadrature by parts
Before a birth of calculus, how to solve areas/volumes of a solid figure made up of smooth curves was referred to as quadrature by parts. Different from calculus, this method depends on figure types so as to successfully achieve clever solutions specific to the types.
In the times of the ancient Greek, Archimedes (278-212 B.C.) demonstrated "An area 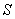 of a parabola
of a parabola 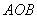 is 4/3 times as large as an area of
is 4/3 times as large as an area of 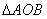 .
.
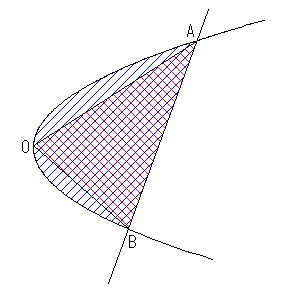
The demonstration is as follows.
Draw the two tangents to the parabola at points 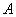 and
and 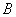 , and the point of intersection between the two is defined as
, and the point of intersection between the two is defined as 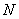 .
.
There is a third tangent parallel to side 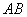 , and the point of intersection between this tangent and the parabola is defined as
, and the point of intersection between this tangent and the parabola is defined as 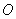 .
.
Produce line 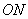 to
to 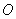 , and the point of intersection between this and the side
, and the point of intersection between this and the side 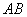 is defined as
is defined as 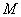 .
.
Then, point 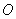 represents the middle point of side
represents the middle point of side 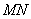 .
.
Therefore an area of 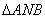
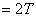
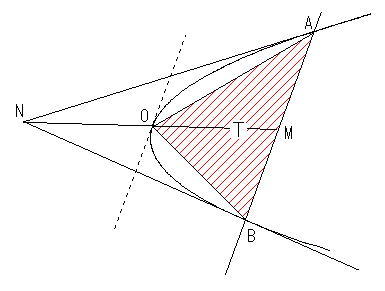
Next, Draw a tangent to the parabola at point 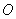 , and the point of intersection between the two is defined as
, and the point of intersection between the two is defined as 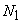 .
.
There is a third tangent parallel to side 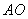 , and the point of intersection between this tangent and the parabola is defined as
, and the point of intersection between this tangent and the parabola is defined as 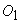 .
.
Produce line 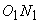 to
to 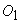 , and the point of intersection between this and the side
, and the point of intersection between this and the side 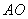 is defined as
is defined as 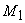 .
.
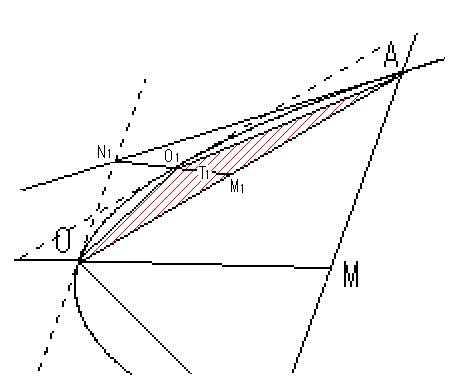
Suppose an area of 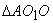 is
is 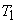 , then an area of
, then an area of 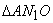
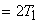 .
.
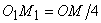
Taking into account another triangle in the side of point 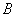 yields
yields 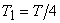 .
.
Such procedure is to be endlessly repeated. However, only infinite times can cover all over the area 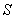 .
.
Archimedes thought as follows:
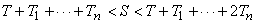
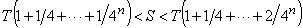
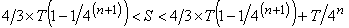
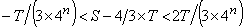
Since  is arbitrary,
is arbitrary,  cannot be but
cannot be but 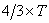 .
.
|
Japanese sites Mathematical Formulas| Kodawari House| Pinpoint StreetView| Excel VBA Techniques| Excel Formula Analysis| |